Reach-Avoid Games | Duy P. Nguyen

This project (Anthony et al., 2022) implements and demonstrates computationally efficient, time-consistent solutions to multi-agent reach-avoid dynamic games, a class of safety-critical optimal control problems where agents aim to reach goal sets while avoiding failure conditions under adversarial or interactive dynamics. These games are widely used as formal models in mobile robot motion planning, autonomous driving, and safety-critical decision making.

Our implementation supports single and multi-player reach-avoid environments, including cooperative and adversarial interactions, with tools for training, evaluation, and visualization.

Core Idea

A reach-avoid game involves agents that must:

Reach a specified target
Avoid unsafe regions or adversarial opponents

Reach-avoid cost is formulated, such that past failures override future successes. The reach-avoid condition for a generic state trajectory $\mathbb{x} = (x_0, \dots, x_T)$ can be expressed as:

\[\exists t \in \{0,\dots,T\} : x_t \in \mathcal{T}_t \wedge \forall \tau \in \{0,\dots,t\} : x_\tau \not\in \mathcal{F}_\tau\]

Solutions are time-consistent, meaning that planned trajectories remain optimal at all timesteps (later control inputs are still optimal despite suboptimal behavior earlier in the trajectory), or time-inconsistent (pinch-point solution).

Highlights & Demos

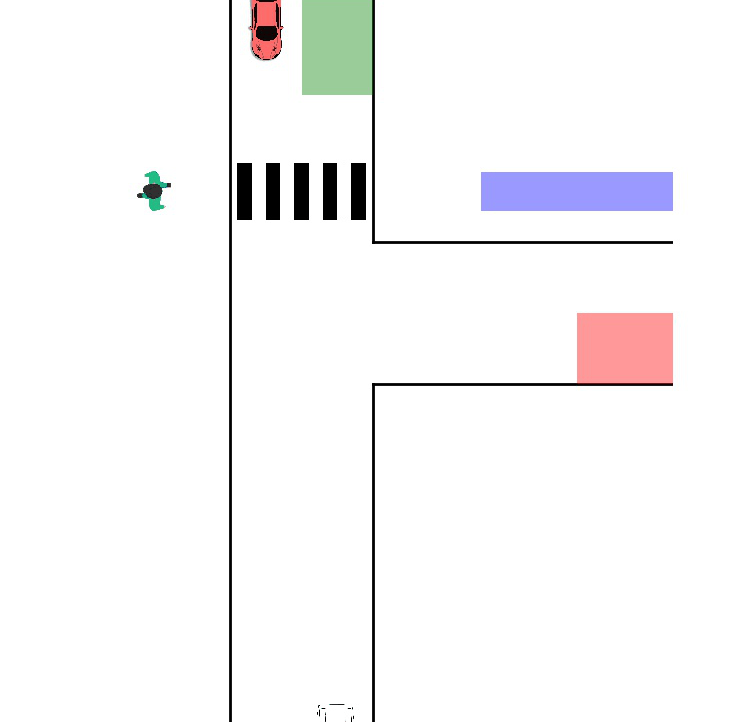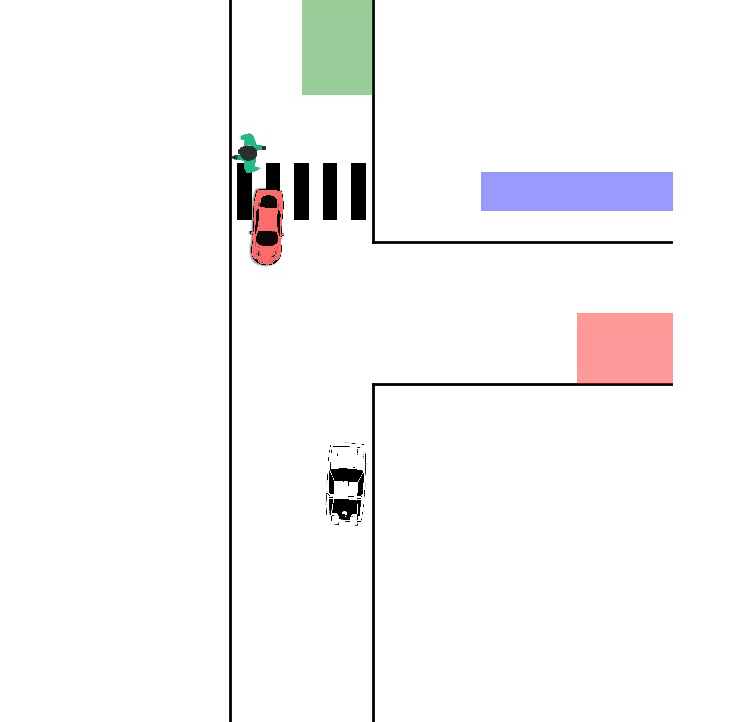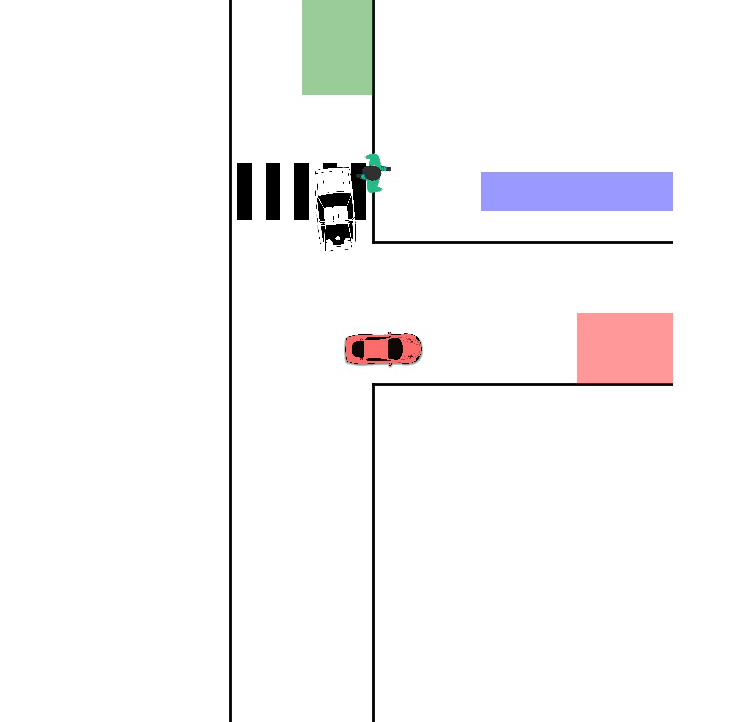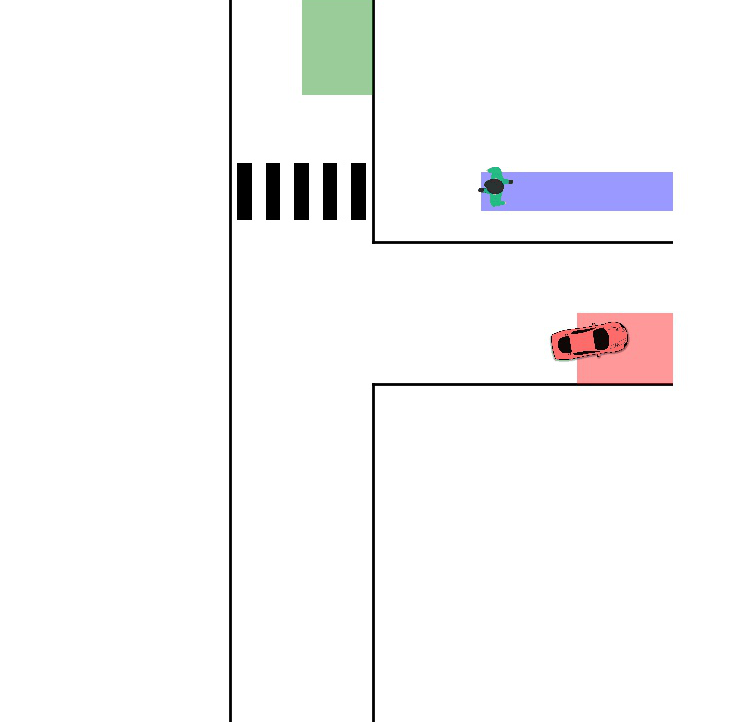
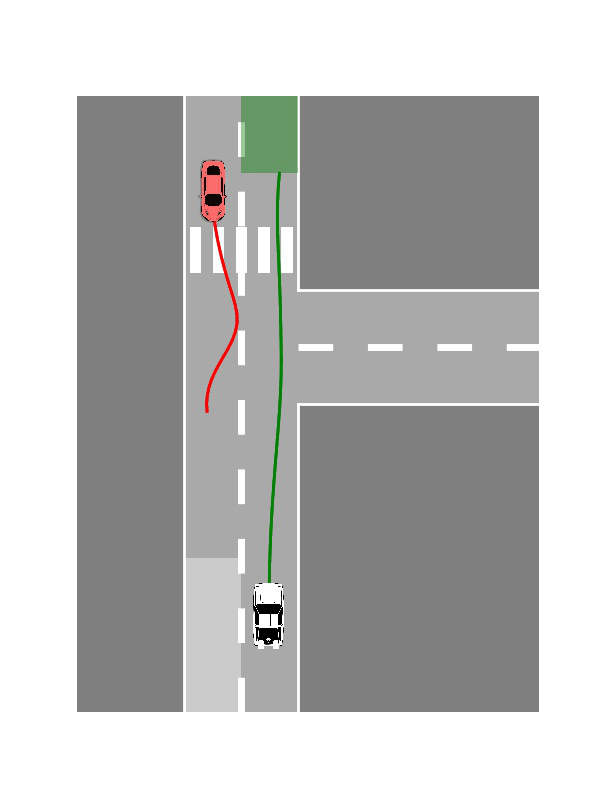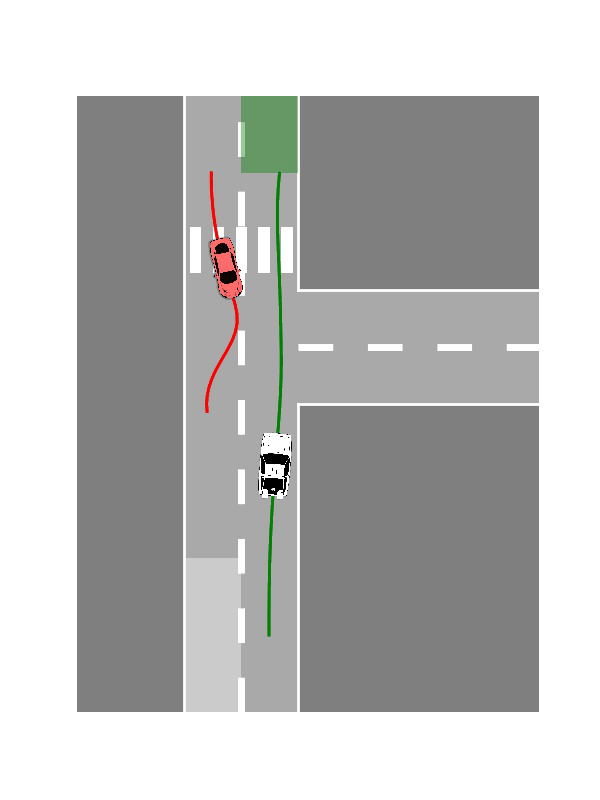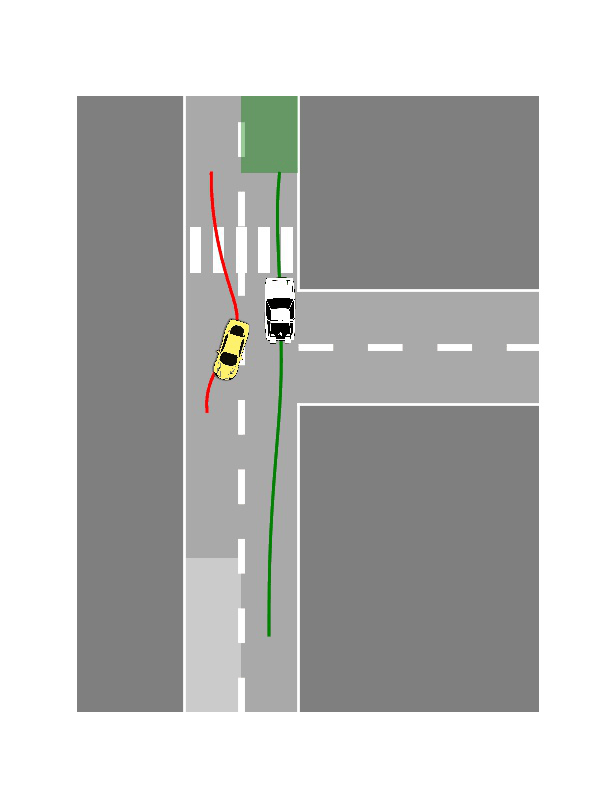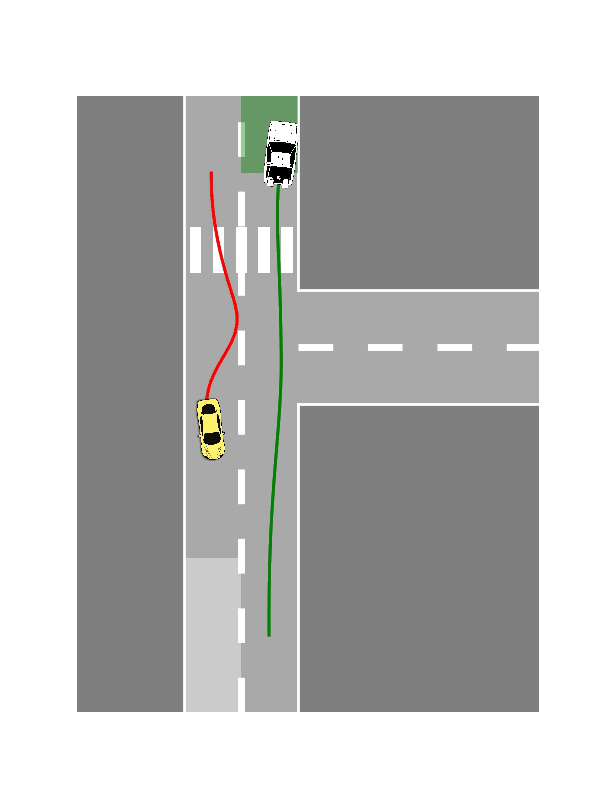
Single-Player Reach-Avoid

One agent navigates a free space with obstacles toward a goal while maintaining safety constraints. We show the result from both time-inconsistent (pinch-point) and time-consistent solution:

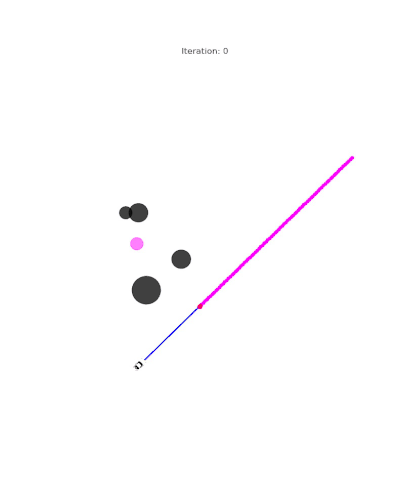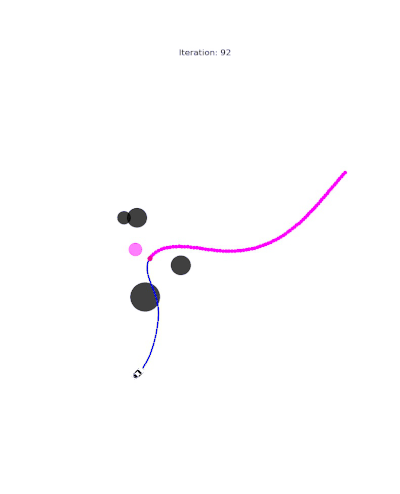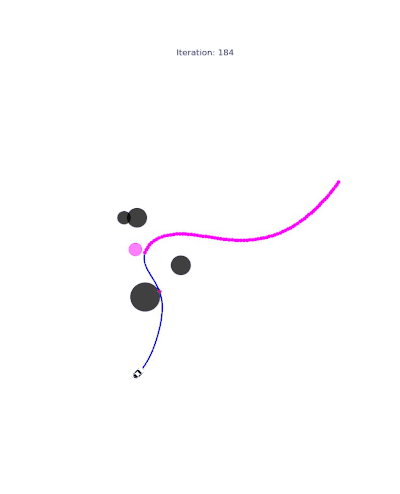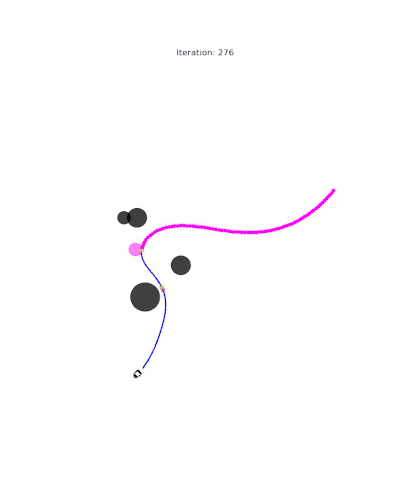
RAG time-inconsistent single-agent training

RAG time-consistent single-agent training

Figure: Time-inconsistent (left) and time-consistent (right) solution for reach-avoid games of single-agent.

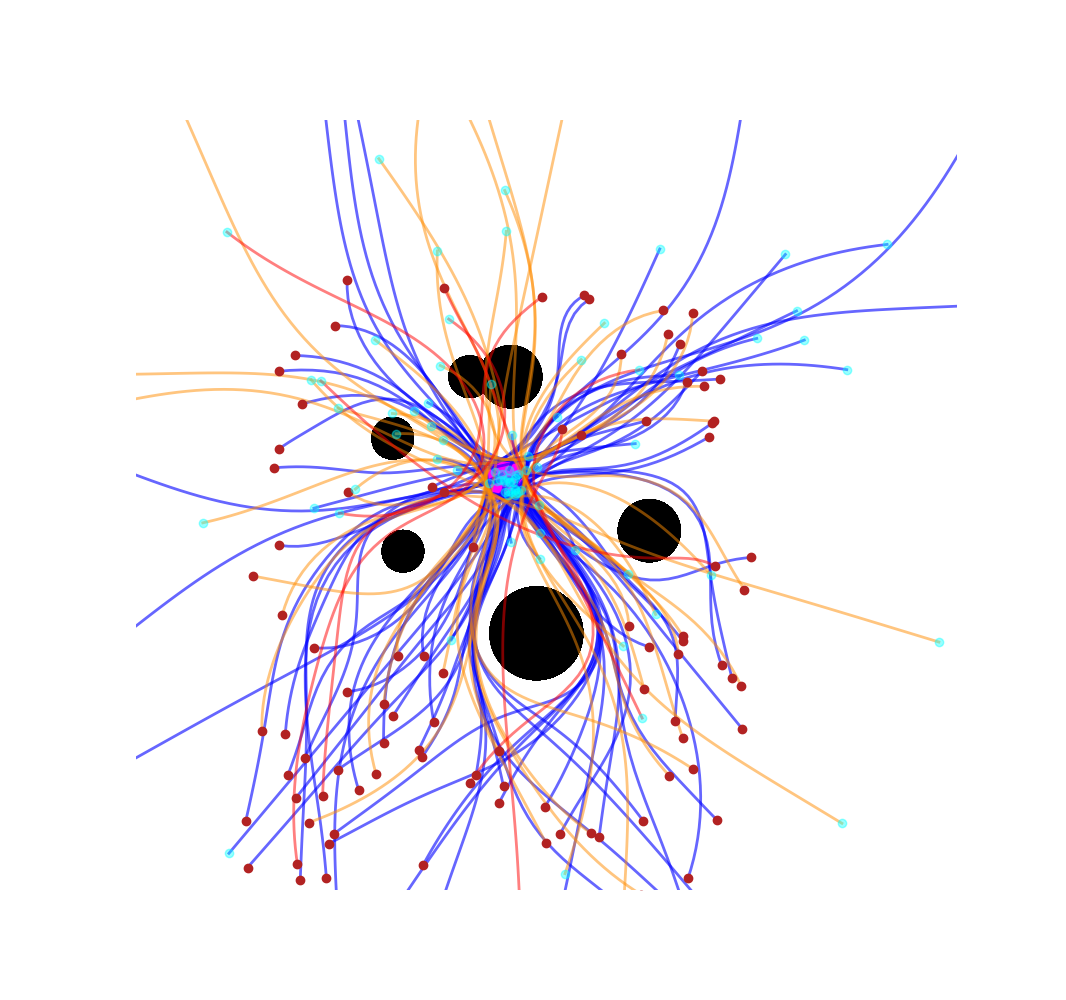
RAG time-inconsistent single-agent training, batch

RAG time-consistent single-agent training, batch

Figure: Batch run of time-inconsistent (left) and time-consistent (right) solution for reach-avoid games of single-agent.

Multi-Player Scenarios

Two-Player Interactions: Cooperative or adversarial reach-avoid dynamics
Three-Player Games: Complex interaction patterns demonstrating scalable behavior synthesis

Figure: Reach-avoid games solution for two-player adversarial scenario (left) and three-player scenario (right).

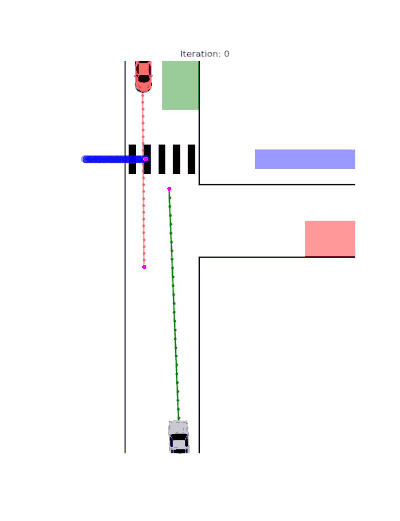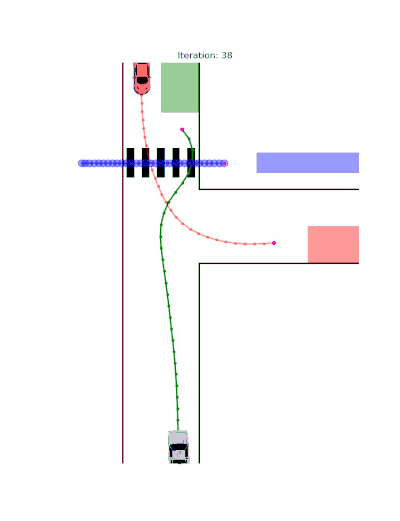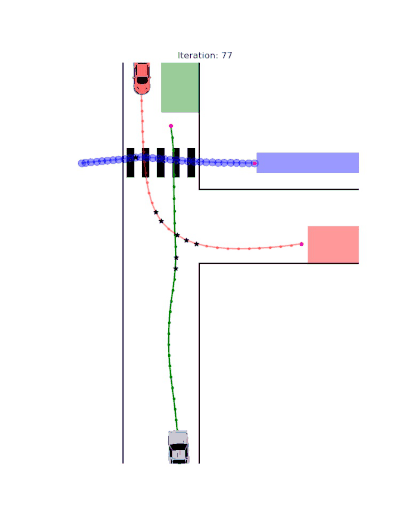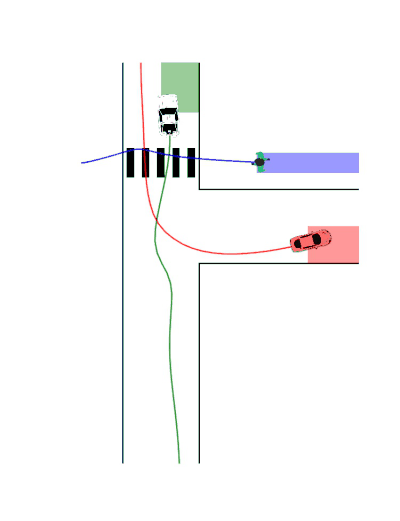
Publication

This work was accepted to ICRA 2022 as Back to the Future: Efficient, Time-Consistent Solutions in Reach-Avoid Games, introducing algorithms for efficiently computing solutions that remain optimal under execution perturbations.

We study the class of reach-avoid dynamic games in which multiple agents interact noncooperatively, and each wishes to satisfy a distinct target criterion while avoiding a failure criterion. Reach-avoid games are commonly used to express safety-critical optimal control problems found in mobile robot motion planning. Here, we focus on finding time-consistent solutions, in which future motion plans remain optimal even when a robot diverges from the plan early on due to, e.g., intrinsic dynamic uncertainty or extrinsic environment disturbances. Our main contribution is a computationally-efficient algorithm for multi-agent reach-avoid games which renders time-consistent solutions for all players. We demonstrate our approach in two- and three-player simulated driving scenarios, in which our method provides safe control strategies for all agents.

Core Idea

Highlights & Demos

Single-Player Reach-Avoid

Multi-Player Scenarios

Publication

References

2022